Two-dimensional percolation model
Contents
Two-dimensional percolation model#
What is percolation model?#
In percolation theory, bonds between lattice points open with probability \(p\), then two points are connected. We discuss the clusters that are then formed, their size, and their dependence on the probability. It is known from extensive research to date that as the probability of the opening of bonds between lattice points is increased, a phase transition phenomenon is observed in which clusters have formed that spread throughout the entire system with a certain probability \(p_{\mathrm{c}}\). The value of this critical probability \(p_{\mathrm{c}}\) is known for many two-dimensional lattices.
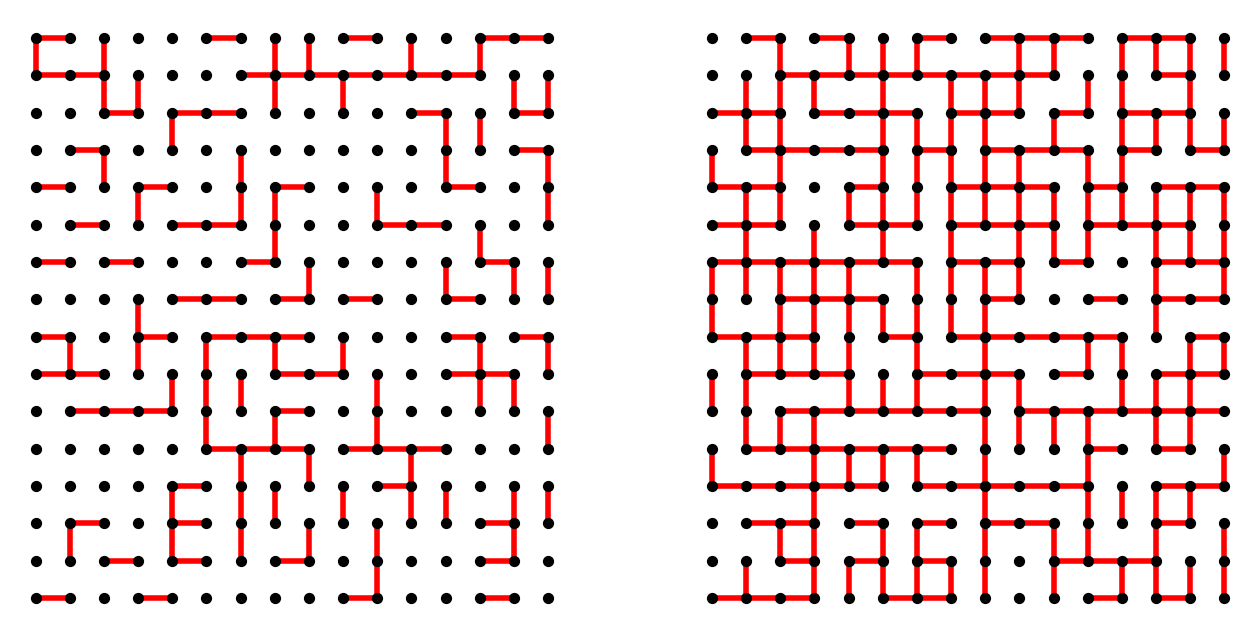This image shows the typical bond percolation configurations on a square lattice with bond probabilities \(p = 0.3\) (left) and \(p = 0.6\) (right) for the lattice size \(L = 16\).
At \(p = 0.\), there are no clusters spread throughout the system.
When \(p = 0.6\) exceeds the critical probability \(p_{\mathrm{c}} = 1/2\), clusters spreading throughout the system, i.e., clusters crossing up and down, or left and right, can be confirmed.
!head data/percolation.txt
64 0.271738670965139 4.919437011718750 0.010667233892421
64 0.280577505729971 5.345457519531250 0.012089049468589
64 0.289416340494803 5.815872070312500 0.013949850107465
64 0.298255175259635 6.368562500000000 0.016178269794194
64 0.307094010024467 6.998375000000000 0.019120008827112
64 0.315932844789299 7.732725097656250 0.022902534314572
64 0.324771679554130 8.589175781250001 0.027863796621939
64 0.333610514318962 9.569217773437501 0.033826930772365
64 0.342449349083794 10.727242187500000 0.041603401658296
64 0.351288183848626 12.126527832031250 0.051040497393409