Skip to content

2021

Gram行列の固有値の数値計算

カーネル関数\(k(\cdot,\cdot)\)が与えられたとき、データ点\(\{x_{i}\}_{i=1}^{n}\)に対するGram行列(グラム行列)は $$ K=\begin{pmatrix}k(x_{1},x_{1}) & \cdots & k(x_{1},x_{n})\\\vdots & \ddots & \vdots\\ k(x_{n},x_{1}) & \cdots & k(x_{n},x_{n})\end{pmatrix} $$ で与えられます。色々な場面に登場するのですが、RBFカーネルからガウス過程を生成する際にその固有値計算で詰まったところがあったのでかんたんにまとめておきます。

Laplacianの積分表現

領域\(\Omega\subset\mathbb{R}^{n}\)上で定義された関数\(u\in C^{2}(\Omega)\)についてLaplacian(ラプラシアン)は $$ \Delta u(x)=\sum_{i=1}^{n}\frac{\partial^{2}u}{\partial x_{i}^{2}}(x) $$ で表されます。このとき、\(\partial B(x,r)=\{y\in\mathbb{R}^{n}\mid |x-y|=r\}\)とおくと、 $$ \Delta u(x)=\lim_{r\to+0}\frac{2n}{r^{2}|\partial B(x,r)|}\int_{\partial B(x,r)}u(y)-u(x)d\sigma_{y} $$ が成り立ちます。\(d\sigma_{y}\)は\(\partial B(x,r)\)上の面積要素です。 この表現を得るには\(u(y)\)を\(x\)まわりでTaylor展開することが大事になるのですが、 その際、平均値の定理によって得られるTaylor展開だと剰余項の評価が難しくなります。 積分型のTaylor展開を用いることでこの問題を解決することができます。

Borwein integral

Borwein積分は\(\sin x/x\)に関する興味深い性質を持った積分のことです。 例えば $$ \int_{0}^{\infty}\frac{\sin x}{x}dx=\frac{\pi}{2} $$ となることはよく知られていますが、これに\(\sin(3x)/3x\)をかけたものについても $$ \int_{0}^{\infty}\frac{\sin x}{x}\frac{\sin (x/3)}{x/3}dx=\frac{\pi}{2} $$ が成り立ちます。同様のことは\(\sin (x/5)/(x/5)\)や\(\sin(x/7)/(x/7)\)をかけていっても成り立ち、 $$ \int_{0}^{\infty}\frac{\sin x}{x}\frac{\sin (x/3)}{x/3}\cdots\frac{\sin (x/13)}{x/13}dx=\frac{\pi}{2} $$ となります。しかし、次のステップではこの計算は崩れて $$ \int_{0}^{\infty}\frac{\sin x}{x}\frac{\sin (x/3)}{x/3}\cdots\frac{\sin (x/15)}{x/15}dx=\frac{467807924713440738696537864469}{935615849440640907310521750000}\pi<\frac{\pi}{2} $$ となってしまいます。一見するとこの値も\(\pi/2\)になりそうなのですが、何故か値がずれてしまいます。 このような積分のことをBorwein積分とよび、いくつかの計算がなされています。

Good Will Hunting Problem

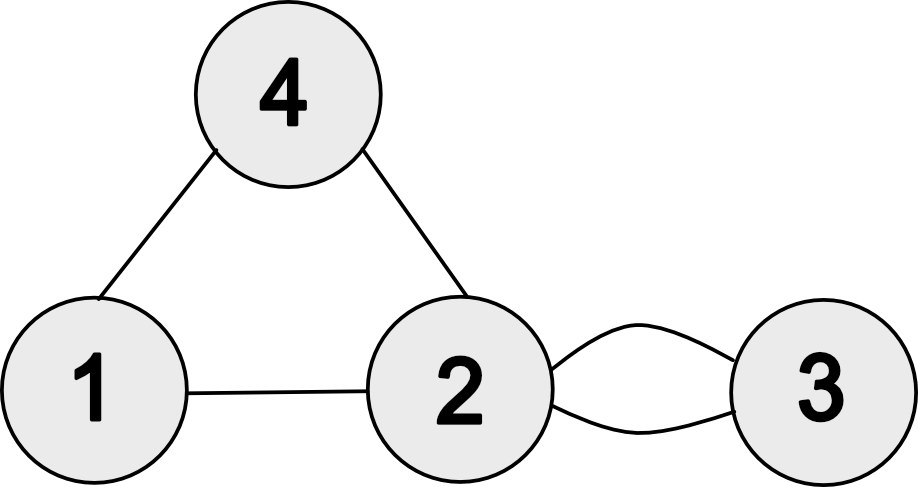
マット・デイモンとロビン・ウィリアムズ主演の映画『グッド・ウィル・ハンティング/旅立ち』(Good Will Hunting)の中で、MITの廊下に掲示されたグラフ理論の問題を清掃をしていたマット・デイモンが解いてしまうシーンがあります。 中学生とかのときに初めてこの映画を見たときにはよっぽど難しい問題なんだろうな、と思ったのですが、最近見返してみると定義に従って素直に計算すれば解ける問題だということがわかったのでまとめておきます。

Quote

Given the graph \(G\), find

  1. The adjacency matrix, \(A\)
  2. The matrix giving the number of 3 step walks
  3. The generating function for walks from \(i\to j\)
  4. The generating function for walks from \(1\to3\)

特異値分解

行列\(A\)を\(m\times n\)の実行列とします。 このときある直交行列\(U\in\mathbb{R}^{m\times m},V\in\mathbb{R}^{n\times n}\)が存在して、 $$ U^{\mathsf{T}}AV=\Sigma=\begin{pmatrix}\mathrm{diag}(\sigma_{1},\dots,\sigma_{r}) & O_{r\times(n-r)} \\ O_{(m-r)\times r} & O_{(m-r)\times (n-r)}\end{pmatrix}\in\mathbb{R}^{m\times n} $$ となるようにできます。このような分解を特異値分解と言います。

至るところ微分不可能な連続関数: 初等的な構成方法

\([-1,1]\)上の関数 $$ \varphi(x)=|x| $$ を考え、 これを\(\varphi(x+2)=\varphi(x)\)として\(\mathbb{R}\)上へ拡張します。 このとき、 $$ f(x)=\sum_{n=0}^{\infty}\left(\frac{3}{4}\right)^{n}\varphi(4^{n}x) $$ は\(\mathbb{R}\)上の連続関数ですが至るところ微分不可能であることが知られています。 以下でこれを示していきましょう。

坂口-蔵本モデルのダイナミクス

坂口-蔵本モデルは蔵本モデルにphase lagを導入したモデルで、次の微分方程式で表されます。 $$ \frac{d\theta_{i}}{dt}=\omega_{i}+\frac{K}{N}\sum_{j=1}^{N}\sin(\theta_{j}-\theta_{i}+\alpha),\quad i=1,\dots,N. $$ \(\alpha\)が位相差に対応していて、\(\alpha=0\)のときは蔵本モデルに戻ります。 結合強度\(K\)が変化したときに振動子が同期するかどうかを調べていきましょう。

包除原理

測度空間\((X,\mathcal{B},\mu)\)の有限測度集合\(A_{i}(i=1,\dots,n)\)に対して $$ \mu\left(\bigcup_{i=1}^{n}A_{i}\right)=\sum_{J\subset[n];J\ne\emptyset}(-1)^{|J|-1}\mu\left(\bigcap_{i\in J}A_{i}\right) $$ が成り立ちます。これを包除原理(Inclusion-exclusion principle)と呼びます。