Unique lifting property

Hatcherの"Algebraic Topology"のProposition 1.34でUnique lifting propertyとその証明が与えられているのですが、その証明がわかりにくかったのでここに分かりやすくまとめてみます。 Hatcherが全体的に読みにくいと感じるのは自分だけだろうか。。。

Unique lifting property¶

Unique lifting propertyは被覆空間によってリフトされた連続写像が一点を決めれば一意に定まることを主張しています。

Theorem: Unique lifting property

被覆写像$p\colon \tilde{X}\to X$と連続写像$f\colon Y\to X$が与えられている。また、$Y$は連結であるとする。 $f$のリフト$\tilde{f} _{1},\tilde{f} _{2}\colon Y\to\tilde{X}$がある一点で同じ値を取るとき、$\tilde{f} _{1}=\tilde{f} _{2}$である。

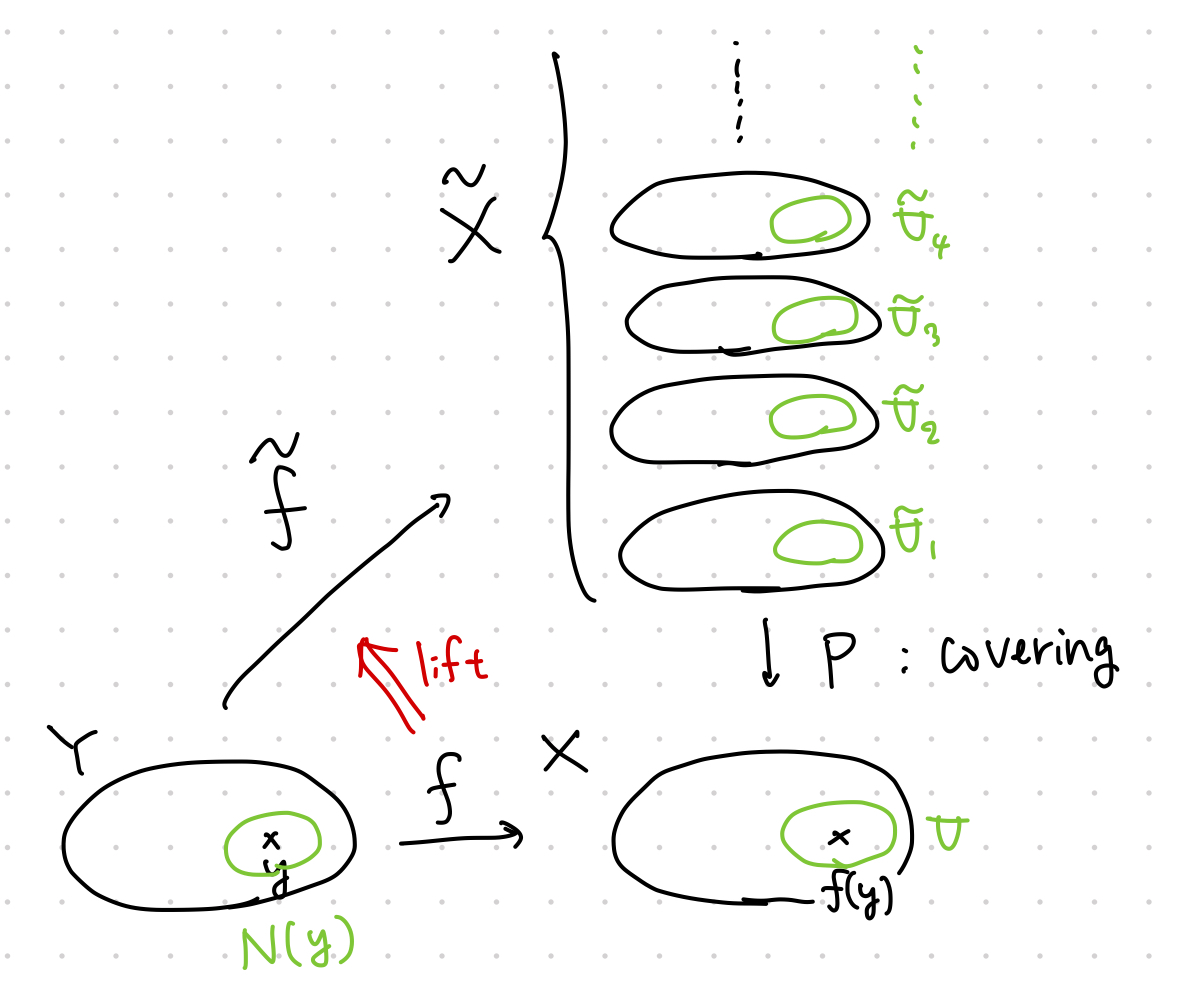
この証明は$Y$が連結であることを巧妙に使います。証明に用いる概略図を以下に示します。

Proof

はじめに被覆空間にまたがる性質を見る。 $y\in Y$に対して$U\subset X$を均一な被覆を持つ$f(y)$の開近傍とする。すなわち、$p^{-1}(U)=\bigcup_{\lambda\in\Lambda}\tilde{U} _ {\lambda}$で$\tilde{U} _ {\lambda}$は互いに素な集合となっていることである。このとき、$\left.p\right| _ {\tilde{U} _ {\lambda}}\colon\tilde{U} _ {\lambda}\to U$が同相写像となる。今リフトは連続であるから、$y$のある開近傍$N(y)$が存在して、 $$ \tilde{f} _ {1}(N(y))\subset \tilde{U} _ {1},\quad \tilde{f} _ {2}(N(y))\subset \tilde{U} _ {2} $$ なるような$\tilde{U} _ {1},\tilde{U} _ {2}\in\bigcup_{\lambda\in\Lambda}\tilde{U} _ {\lambda}$が存在する。

$Y$を次の互いに素な部分集合$Y_{1},Y_{2}$に分割する。 $$ \begin{aligned} &Y_{1}=\{y\in Y\mid \tilde{f} _ {1}(y) = \tilde{f} _ {2}(y)\}\\ &Y_{2}=\{y\in Y\mid \tilde{f} _ {1}(y) \neq \tilde{f} _ {2}(y)\} \end{aligned} $$ はじめに$Y_{1},Y_{2}$がともに開集合であることを示す。

$Y_{1}$が開集合であることを示す。$y\in Y_{1}$であれば、 $\tilde{f} _ {1}(y)\in\tilde{U} _ {1}, \tilde{f} _ {2}(y)\in\tilde{U} _ {2}$であるから$\tilde{U} _ {1}$と$\tilde{U} _ {2}$は共通部分を持つ。 $\tilde{U} _ {\lambda}$は互いに素であるから、共通部分を持つなら$\tilde{U} _ {1}=\tilde{U} _ {2}$である。よって、上で定義した$y$の開近傍$N(y)$について、$N(y)$上で2つのリフトは一致するので$N(y)\subset Y_{1}$となる。これは任意の$y\in Y_{1}$について成り立つから$Y_{1}$は開集合である。
$Y_{2}$が開集合であることを示す。$\tilde{f} _ {1}(y)\ne\tilde{f} _ {2}(y)$だが、$p(\tilde{f} _ {1}(y))=p(\tilde{f} _ {2}(y))=f(y)$である。 $f(y)$を含む$U$について$\left.p\right| _ {\tilde{U} _ {\lambda}}\colon\tilde{U} _ {\lambda}\to U$が同相写像であることから、 $\tilde{f} _ {1}(y),\tilde{f} _ {2}(y)$それぞれを含む$\tilde{U} _ {1},\tilde{U} _ {2}$はそれぞれ異なる集合であることがわかる。よって、$y$の開近傍$N(y)$について、$N(y)$上で2つのリフトは一致しないので$N(y)\subset Y_{2}$となる。これは任意の$y\in Y_{2}$について成り立つから$Y_{2}$は開集合である。

よって、$Y=Y_{1}\cup Y_{2}$であり、$Y_{1}$と$Y_{2}$は開集合であることがわかった。$Y$は連結であるから、$Y_{1}$と$Y_{2}$のいずれかが空集合である。今、ある一点で$\tilde{f} _ {1},\tilde{f} _ {2}$が同じ値であるから$Y_{1}$は空ではない。よって$Y=Y_{1}$であり、$\tilde{f} _ {1} = \tilde{f} _ {2}$が示された。